I saw an article some days ago where the author claimed that If the current growth of Chrome will remain at a steady pace for the next few months, […] it will surpass Firefox in around last quarter of 2011
. Although I prefer Chrome to other browsers and use it daily, I cannot agree with this assessment, especially since the author doesn’t make his numbers public. Chrome has indeed grown at a steady pace in the last months, but the rate is nowhere near enough to catch up to Firefox until the end of next year. Not there is any guarantee the current growth will continue. And people have been overestimating Chrome’s growth ever since it was launched: this article on TechCrunch predicted it will catch up to Firefox in two years, which obviously didn’t happen.
Nevertheless, the article made me wonder if I could do a better job of predicting the short term evolution of browsers. A linear trend is not really suited in this case: extending it too far into the future will lead to nonsensical results, because market share cannot grow beyond 100% or shrink under 0%. A better representation would be the Markov chain, a model I learned about in college aimed at predicting the evolution of products on a competing market. It starts with a simple assumption: in the next period, a user can either stick with the same product – in this case browser – or switch to one of the others. The probabilities for these actions are summed up in a n by n matrix that can be used to predict future market share or even a ‘steady state’, a market equilibrium, if nothing disrupts the current evolution.
The obvious problem here is to determine this Markov probability matrix. I won’t go into all the details about the calculation, just the rough method and some results. I started with the worldwide browser share statistic from StatCounter for the last two years on a weekly basis. I chose weeks instead of months because it gives access to a larger number of data points and it’s also more uniform: weeks have the same number of days and weekends throughout the year. I also added Opera under ‘Other browsers’ to simplify things, since it didn’t have much of an evolution in that period. I used the Solver in Microsoft Excel to find the Markov matrix that would best fit these data. You can see the calculations and some other variations based on monthly data from both StatCounter and NetApplications in this Google Docs spreadsheet.
One of the models fits the data from the last year particularly good. Extending it until the end of the year gives a predicted market share of 49.2% for Internet Explorer, 30.3% for Firefox and 13.5% for Chrome. Firefox is hitting an all-time high these weeks and starts a slow decline. You can theoretically extend the forecast as far in the future as you like: the end of 2011 for example should see the following market share situation: Internet Explorer - 44.2%, Firefox - 28.2%, Chrome - 20.8% and Safari - 4.4%. So Chrome is nearing Firefox, but still not “eclipsing” it. 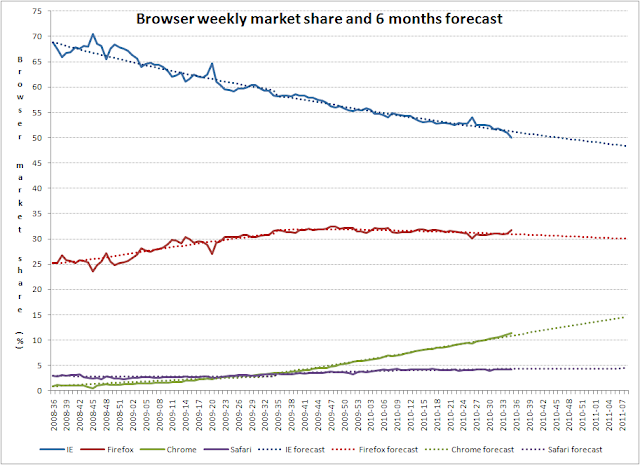
It’s also interesting to examine the Markov matrix, because it shows how users are migrating from browser to browser, at least according to the model:
- Internet Explorer has a pretty loyal user base: 99.3% of it’s users will stay with Internet Explorer the next week – whether they choose it or not is another matter. Most of the rest migrate to Firefox. Surprisingly, the model shows 8.9% of users actually migrate to Internet Explorer from ‘other browsers’. Maybe that explains why it’s so hard to get rid of it’s older versions…
- Only 98% of Firefox users will be using the browser the following week, but Firefox compensates by attracting a larger portion (10.1%) from the ‘other browsers’;
- Chrome has by far the most loyal users: according to the model, none of them switch away after adopting Chrome! While this may be due to rounding, it can be good explanation for the steady growth of Google’s browser. Chrome also attracts 2.1% of Safari’s users each period and small percentages (0.1%) from Firefox and Internet Explorer;
- Safari manages to retain only 97.8% of users and attracts others from Firefox and ‘other browsers’.
The Markov model, while easy to use, clearly has some disadvantages that make it’s use limited in real life forecasts. The biggest is the assumption that the migration matrix remains unchanged all the time, so it doesn’t take into account changes in user preferences caused by new browser versions or the launch of new competitors. I don’t have any numbers to check, but I imagine the introduction of Google Chrome two years ago would have thrown all such models off tracks. With the biggest players, Firefox and Internet Explorer, preparing to launch new major versions probably by the end of the year, it remains to be seen if this forecast will remain relevant or if these updates will change the trends set in the last year.
2 comments:
Could you share how you use solve to produce the transition matrix?
Well, I set it up like this:
1. I have the actual market share percentages in a couple of columns;
2. then in another set of columns the predicted percentages based on a baseline month multiplied with the transition matrix for each new prediction;
3. somewhere in a corner I place the transition matrix and populate it with random numbers, between 0 and 1;
4. finally another column where for each month I calculate the sum of squared differences between actual and predicted market share per browser;
5. and a cell where I sum up all the values from this latter column.
And now for the Solver part:
1. in Solver set the sum from point 5 above to 'minimize';
2. Set the cells containing the transition matrix as 'Variable cells';
3. Add constraints for the transition matrix to only have numbers between 0 and 1 (0% to 100%).
Then I run solver a couple of times until I find the lowest value for the result in point 5, this should be the best match for the transition matrix.
Hope this helps!
Post a Comment